
Este trabalho de iniciação Científica
tem como objetivo aplicar uma heurística construtiva ao problema
de cortes. Através da heurística podemos gerar, combinar
e selecionar soluções de subproblemas em relação
ao problema original, de modo que se consiga se aproximar da solução
ótima. Primeiramente esta heurística será aplicada
em problemas de cortes regulares guilhotinados, e posteriormente o corte
não guilhotinado.
A proposta de aplicar uma heurística construtiva ao Problema de Cortes Regulares está apresentada nos próximos tópicos. Inicialmente os problemas são apresentados e colocados em uma notação padronizada; em seguida são descritos exemplos de aplicações práticas para os mesmos.
A heurística é então desenvolvida e mostrada de forma que seja suficientemente conhecida sua forma geral onde são geradas, combinadas e criteriosamente selecionadas as soluções para subproblemas em relação ao problema original, até que se construa uma solução para este último. A heurística será apresentada de forma idêntica para os dois problemas em questão, sendo que a diferença só irá aparecer na forma como os cálculos dos parâmetros serão implementados.
Posteriormente serão desenvolvidas aplicações tanto para testes em plataformas menores, como microcomputadores, como para estações de trabalho de maior porte, dependendo do tamanho e da complexidade das instâncias de teste.
É dada ainda uma superfície bi-dimensional com altura e largura fixa. O objetivo do problema é criar uma distribuição onde todos os blocos sejam alojados nesta superfície com a menor perda interna possível.
As peças não tem orientação
fixa e podem ser giradas em 90o. Foi utilizada ainda a restrição
que esta distribuição deve gerar um esquema guilhotinável.
Uma distribuição é dita guilhotinável se e
somente se ela pode ser criada bipartindo recursivamente a superfície
com cortes retos.
Estes problemas podem ser aplicados a uma série de situações práticas aonde se faz necessário determinar qual é a melhor forma de se distribuir um determinado número de peças sobre uma determinada superfície limitada.
III.1 Indústrias de madeira ou aço
Nesses têm-se grandes placas de aço ou madeira a partir da qual devem ser feitas peças para uma aplicação qualquer. O problema de cortes se aplica nestas situações para determinar qual é o padrão de corte no qual é o padrão de corte no qual ocorre o menor desperdício de matéria prima possível.
Exemplos de indústrias que seriam beneficiadas são: Indústria de produção de móveis em massa e indústria de construção naval.
A heurística aplicada nesta proposta se baseia no artigo "A Dynamic List Heuristic for 2D-Cutting" ( Lorena e Lopes, 1996) [1] e na proposta de tese de doutorado "Uma Nova Heurística Construtiva e suas Aplicações à Problemas de Otimização Combinatória"(Furtado, 1996) [2].
IV.1 - Visão Geral.
Dada uma placa de altura fixa ![]() e
comprimento
e
comprimento ![]() ,
e um conjunto
,
e um conjunto ![]() de
n
peças a serem distribuídas sobre esta superfície.
Essas peças devem ser retangulares. As peças devem ser distribuídas
em uma seqüência que faça com que o comprimento, denominado
de
n
peças a serem distribuídas sobre esta superfície.
Essas peças devem ser retangulares. As peças devem ser distribuídas
em uma seqüência que faça com que o comprimento, denominado ![]() ,
seja o menor possível. A heurística se consiste em manter
uma lista de seqüências usando subconjuntos de I
e, iterativamente, selecionar dois elementos desta lista, combiná-los
e assim gerar uma nova seqüência, aumentando portanto o total
de soluções na lista.
,
seja o menor possível. A heurística se consiste em manter
uma lista de seqüências usando subconjuntos de I
e, iterativamente, selecionar dois elementos desta lista, combiná-los
e assim gerar uma nova seqüência, aumentando portanto o total
de soluções na lista.
A cada interação, além da geração de novos elementos, é feita a eliminação dos elementos que não satisfaçam a um critério determinado para a permanência na lista.
Guardando-se a melhor seqüência encontrada até o momento, o processo termina quando a lista fica vazia ou um número máximo de iterações é atingindo.
IV.2 - Algoritmo de Distribuição das peças
Antes de falar em como as peças são distribuídas
sobre a superfície, deve-se definir como é representada uma
seqüência de peças, que na verdade é uma solução
particular deste problema. A solução aproximada
para a distribuição das peças de um subconjunto de
I
é representada por um vetor Sk, cujo número
de elementos é igual ao número total de peças n,
de modo que Sk[I] = j significa que na seqüência
K, a i-ésima peça será a j-ésima a ser colocada
sobre a superfície. Caso Sk[i] = 0, a i-ésima
peça não faz parte da seqüência K. É importante
frisar que Sk[i] = Sk[j] ![]() 0
se e somente se i = j, isto é, não podem haver elementos
repetidos neste vetor a menos que este elemento seja 0. Outra consideração
a ser feita é que o valor de Sk[I] deve estar entre 0
e n.
0
se e somente se i = j, isto é, não podem haver elementos
repetidos neste vetor a menos que este elemento seja 0. Outra consideração
a ser feita é que o valor de Sk[I] deve estar entre 0
e n.
Para o caso das peças retangulares, a técnica para a disposição das mesmas é bastante simples. Cada peça sempre é colocada na posição mais a esquerda e mais baixa possível, nesta ordem de prioridade. Desta forma a primeira peça sempre será colocada no canto inferior esquerdo da placa, e as seguintes serão colocadas sobre a primeira, formando uma coluna. Quando não for mais possível colocar uma peça dentro desta coluna, a próxima peça da seqüência será colocada na parte de baixo da placa, ao lado da coluna anterior, e irá começar uma nova coluna. A largura e a altura de cada coluna são dadas respectivamente pela largura da peça mais larga da coluna em questão, e pelo somatório de todas as peças que compõe a mesma.
Para cada peça colocada é feita a avaliação da área desperdiçada para a peça colocada na posição original e para a peça rotacionada. Caso a rotação gere um desperdício menor, será feita uma inversão dos parâmetros altura e largura da peça em questão e somente depois ele será posicionada. Na figura IV.l encontra-se o pseudo código para este algoritmo.
Como as peças sempre estão dispostas em
colunas, o algoritmo acima gera soluções guilhotináveis,
mas pode trazer grandes perdas de espaço, visto que ele não
permite que duas peças sejam colocadas lado a lado dentro de uma
mesma coluna. Por esse motivo a seqüência na qual as peças
são colocadas é fundamental, e a heurística construtiva
vai escolher qual a melhor seqüência a ser utilizada.
Figura IV.1 - Pseudo código do Algoritmo para distribuição
das peças retangulares
IV.3 - Lista de Soluções para os Subconjuntos
Cada elemento da lista de soluções armazena três
informações sobre o subconjunto dos clientes: uma solução
aproximada para a ordem dos clientes distribuídos, um limiar
para a retirada desse elemento da lista e um valor de referência
para a ordenação dos elementos na lista.
Em cada elemento da lista, a solução aproximada
é o vetor ![]() descrito
no item IV.2. Seja agora S o conjunto de todas as sequências
descrito
no item IV.2. Seja agora S o conjunto de todas as sequências ![]() ,
ou seja,
,
ou seja, ![]() ,
onde m é o número de sequências.
,
onde m é o número de sequências.
Sejam ainda as funções ![]() e
e ![]() ,
duas funções que mapeiam uma sequência
,
duas funções que mapeiam uma sequência ![]() em
em ![]() ,
de forma que
,
de forma que ![]() seja
um limite superior para
seja
um limite superior para ![]() ,
ou seja,
,
ou seja,
![]() onde (IV.1)
onde (IV.1)
![]()
figura IV.2 - Representação gráfica do conjunto
S e das funções f(sk), g(sk) e gmax
Definimos agora, para o problemas de cortes, a função f para cada elemento do conjunto de soluções S.
![]() , p/k =
1,2,...,m
, p/k =
1,2,...,m
onde
![]()
Abaixo encontra-se um exemplo de um caso, sendo que a área preenchida da corresponde ao valor da função f(sk).
Para o problema de cortes a função g
é definida como,
figura IV.4 - Representação gráfica
da função g(Sk) para o exemplo anterior
Como no algoritmo utilizado em cortes irregulares as peças
não são dispostas em colunas, é necessário
fazer a distribuição das peças, dividir o comprimento
total em um certo número de colunas e depois verificar dentro de
cada coluna gerada qual peça pertencente a mesma possui a maior
coordenada y. Desta forma, tendo a altura e a largura das colunas calcula-se
a área total.
O valor de gmax é calculado
através da seguinte função:
![]()
onde: mult Þ fator para garantir que gmax > g(sk) para k = 1,2,...,m.
CP max Þ comprimento
de um caso particular utilizando todas as pecas do conjunto I.
É importante observar que o valor de gmaxé
calculado apenas uma vez, no início do processo.
O desvio absoluto, que no caso dos problemas de cortes
é dado pela área não ocupada por nenhuma peça,
é claramente calculado pela diferença g(sk)
-f(sk). Em termos percentuais o desvio é dado por
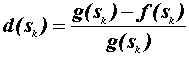
Logo o desvio absoluto pode ser escrito da seguinte forma:
![]()
Existe ainda o parâmetro d, que é
um número fixo em todos os processos, estipulado arbitrariamente
no inicio do mesmo, e que representa o desvio percentual máximo
esperado valor da função que avalia uma solução
aproximada do problema original. Em termos absolutos, portanto, o maior
valor da área que espera-se desperdiçar é dado pela
função ![]() .
.
Para cada solução sk
existe um desvio absoluto, que para este problema é a quantidade
de área que já foi desperdiçada, como já foi
descrito. Também já foi definido o desvio máximo desejado,
que é a maior quantidade de área que permite-se desperdiçar.
Portanto para cada solução também irá existir
uma quantidade área que ainda permite-se desperdiçar, que
é calculada pelo termo ![]() .
.
O valor deste termo diminui conforme o valor de g(sk)
aumenta,
portanto espera-se que este valor diminua conforme vão sendo geradas
sequência que tenham a participação de uma maior numero
de peças. Como deseja-se um resultado melhor do que o máximo
desvio permitido d, espera-se que conforme o valor de g(sk)
se aproxima de gmax, o valor do somatória
do total desperdiçado na solução mais o total que
ainda permite-se perder diminua. Matematicamente, espera-se ter uma diminuição
no termo abaixo:
![]() (IV.8)
(IV.8)
Caso o termo acima se torne maior que o máximo
desvio permitido, ou seja ![]() ,o
desvio da solução em questão se tornou maior do que
o previsto. Introduzimos um parâmetro
,o
desvio da solução em questão se tornou maior do que
o previsto. Introduzimos um parâmetro ![]() que
ira controlar o processo de construção das sequências.
Supõe-se então que se
que
ira controlar o processo de construção das sequências.
Supõe-se então que se
![]() (IV.9)
(IV.9)
a seqüência em questão será retirada
da lista. Se isolarmos a na inequação
poderemos calcular um limiar de retirada para a seqüência
em questão, que é denominado ![]() .
Matematicamente tem-se
.
Matematicamente tem-se
![]() (IV.10)
(IV.10)
A lista é mantida ordenada de forma crescente de
acordo com um valor de referência que também
é guardado em cada elemento da lista, e é dado por
![]() (IV.11)
(IV.11)
onde: ![]() é
o número de peças que entram nesta solução
aproximada.
é
o número de peças que entram nesta solução
aproximada.
Quanto menor o valor de referência ![]() ,
menos peças restam para ser colocados no subconjunto e possivelmente
existirão menos espaços livres na superfície.
,
menos peças restam para ser colocados no subconjunto e possivelmente
existirão menos espaços livres na superfície.
Portanto, de modo geral, cada elemento da lista armazena
a solução aproximada representada pelo vetor ![]() ,
o limiar
,
o limiar ![]() e
o valor de referência para ordenação
e
o valor de referência para ordenação ![]() .
.
IV.4 - Lista Inicial
O processo de seleção e combinação
exige uma lista inicial seja gerada, contendo seqüências geradas
de acordo com algum critério.
Para a lista inicial são geradas n seqüências, onde n é o número total de peças a serem distribuídas. Cada seqüências possui n/2 peças, e para garantir que na lista inicial cada peça apareça em cada uma das posições possíveis, foi usado o esquema para geração que está representado na figura IV.l.
O limiar ![]() deve-se
ao fato de ser necessário manter esses elementos inicias na lista
durante um certo tempo.
deve-se
ao fato de ser necessário manter esses elementos inicias na lista
durante um certo tempo.
Para ter uma melhor idéia da configuração das seqüências iniciais para um caso onde devessem ser distribuídas 8 peças, os vetores ficariam como na figura IV.2.
|
|
|
|
|
|
|
|
|
|
| s1 |
|
|
|
|
|
|
|
|
| s2 |
|
|
|
|
|
|
|
|
| s3 |
|
|
|
|
|
|
|
|
| s4 |
|
|
|
|
|
|
|
|
| s5 |
|
|
|
|
|
|
|
|
| s6 |
|
|
|
|
|
|
|
|
| s7 |
|
|
|
|
|
|
|
|
| s8 |
|
|
|
|
|
|
|
|
IV.5 - Geração de novos seqüências
A cada iteração é gerado um certo número de novas seqüências, e não apenas uma única. Para efeito de testes esse número foi o mesmo que o número de peças no conjunto original, que é também o tamanho da lista original.
O processo de geração de novas seqüências consiste em selecionar duas seqüências já armazenadas na lista e combiná-las.
Uma das seqüências é selecionada aleatoriamente entre os n primeiros elementos da lista, onde n é o número de itens no conjunto original I. Com isso ao menos essa seqüência está certamente entre as melhores da lista, isto é, aquelas onde o desperdício de superfície é menor e existem mais peças na seqüência. Esta seqüência será nomeada seqüência base (Sb). A outra seqüência guia (Sg).
A combinação entre estas duas seqüências para gerar uma nova seqüência (Sl) será feita através do seguinte processo:
1- Determina-se o número de peças que participam da seqüência base (tb) e da seqüência guia (tg);
2- Seleciona-se aleatoriamente uma peça que participe da seqüência guia;
3- Caso esta peça não participe da seqüência base, ou seja, nesta seqüência seu valor seja igual a zero (Sb[k] = 0), a seqüência gerada será igual a seqüência base, sendo que a única diferença é que o elemento selecionado entrará como entrará como próximo elemento da seqüência, ou seja, ele assumirá o valor tb + 1 (Sl [k] = tb+l );
4- Caso a peça selecionada participe da seqüência
base (Sb[k] ![]() 0) e o valor
desta peça na seqüência guia seja menor ou igual ao tamanho
da seqüência base (Sg [k]
0) e o valor
desta peça na seqüência guia seja menor ou igual ao tamanho
da seqüência base (Sg [k] ![]() tb),
a seqüência gerada será igual à seqüência
base, mas o valor do elemento k da seqüência resultante será
o valor deste elemento na seqüência guia (Sl[k] = Sg[k]). Para
o valor de Sb[k] não ser perdido e para o valor Sg[k] não
ficar repetido na seqüência resultante, Sb[k] entra no lugar
do elemento que possui o valor Sg[k] na seqüência base (Sl[I]
= Sb[k], onde Sb[I] = Sg[k]);
tb),
a seqüência gerada será igual à seqüência
base, mas o valor do elemento k da seqüência resultante será
o valor deste elemento na seqüência guia (Sl[k] = Sg[k]). Para
o valor de Sb[k] não ser perdido e para o valor Sg[k] não
ficar repetido na seqüência resultante, Sb[k] entra no lugar
do elemento que possui o valor Sg[k] na seqüência base (Sl[I]
= Sb[k], onde Sb[I] = Sg[k]);
5- Caso a peça selecionada participe da seqüência
base (Sb[k] ![]() 0) e o valor
desta peça na seqüência guia seja maior que o tamanho
da seqüência base (Sb[k] > tb), a seqüência gerada
será igual à seqüência base, sendo que a diferença
é que o elemento selecionado será o próximo elemento
da seqüência (Sl[k] = tb + l), e o valor do elemento substituído
Sb[k] será alocado aleatoriamente para a posição de
uma peça que não participa da sequência base.
0) e o valor
desta peça na seqüência guia seja maior que o tamanho
da seqüência base (Sb[k] > tb), a seqüência gerada
será igual à seqüência base, sendo que a diferença
é que o elemento selecionado será o próximo elemento
da seqüência (Sl[k] = tb + l), e o valor do elemento substituído
Sb[k] será alocado aleatoriamente para a posição de
uma peça que não participa da sequência base.
Abaixo são mostrados casos que ilustram as situações
3, 4 e 5 descritas acima:
| [0] | [1] | [2] | [3] | [0] | [0] | [0] | [0] |
|
| [0] | [0] | [0] | [1] | [3] | [2] | [0] | [0] |
|
| [0] | [1] | [2] | [3] | [0] | [4] | [0] | [0] |
|
| [0] | [1] | [2] | [3] | [0] | [0] | [0] | [0] |
|
| [0] | [0] | [0] | [1] | [3] | [2] | [0] | [0] |
|
| [0] | [3] | [2] | [1] | [0] | [0] | [0] | [0] |
|
| [0] | [1] | [2] | [3] | [0] | [0] | [0] | [0] |
|
| [4] | [0] | [1] | [5] | [3] | [2] | [0] | [0] |
|
| [0] | [1] | [2] | [4] | [0] | [0] | [3] | [0] |
|
IV.6 - Eliminação de Seqüências da lista
Como foi descrito no item IV.3, ![]() é
um parâmetro de controle do método, onde
é
um parâmetro de controle do método, onde ![]() ,
iniciando o processo com valor zero, e sendo incrementado lentamente a
cada iteração.
,
iniciando o processo com valor zero, e sendo incrementado lentamente a
cada iteração.
Como já foi explicado também, toda sempre
que o valor de ![]() se tornar
maior que o limiar de retirada de uma determinada seqüência
Sk, esta seqüência deve ser retirada da lista. Em outras palavras,
retira-se uma seqüência da lista sempre que
se tornar
maior que o limiar de retirada de uma determinada seqüência
Sk, esta seqüência deve ser retirada da lista. Em outras palavras,
retira-se uma seqüência da lista sempre que
![]()
Como já mencionado, ![]() deve
ser incrementado lentamente, mas esse incremento deve ser ainda mais lento
quanto
deve
ser incrementado lentamente, mas esse incremento deve ser ainda mais lento
quanto ![]() ,
para que as melhores seqüência sejam mantidas na lista por mais
tempo.
,
para que as melhores seqüência sejam mantidas na lista por mais
tempo.
IV.7 - Término do processo
O processo procura fazer as combinações de modo que o conjunto original I seja formado com as combinações de subconjuntos, mas não há garanti que a solução ótima seja encontrada. Portanto o método deve manter a salvo a melhor seqüência que contenha todas as peças e serem distribuídas a cada iteração.
O processo iterativo para quando, após pelo menos
uma seqüência que contenha todas as peças a serem distribuídas
existir, a lista ficar vazia ou então um certo número de
iterações for alcançado.
[1]Lorena, L. A. N. e Lopes, F. B. ?A Dynamic List Heurística for 2d-Cutting?
In System Modeling and Optimization, Chapman-Hall, 1996, p. 481-488
[2]Furtado, J. C. ?Uma Nova Heurística Construtiva e sua Aplicação à Problemas de Otimização Combinatória?. (Proposta de Tese de Doutorado em Computação Aplicada), INPE, 1996