INTEGRAÇÃO
DO ALGORITMO DE P-MEDIANAS AO SPRING
Integração ao SPRING
O Sistema de Processamento de Informações
Georeferenciadas [SPRING, 1998][1]
é um sistema computacional desenvolvido pela equipe da Divisão
de Processamento de Imagens (DPI) do Instituto Nacional de Pesquisas Espaciais.
Este sistema objetiva a integração e análise de diferentes
tipos de dados espaciais. O modelo de dados do SPRING está baseado
no paradigma de orientação a objetos [Câmara, 1995][2].
Um banco de dados geográfico é composto de planos de informação,
de objetos geográficos, e de informações não
espaciais. Os planos de informação podem representar informações
contínuas no espaço (campos), ou os objetos geográficos
individuais. Cada plano de informação pode conter representações
espaciais do tipo vetorial ou varredura. A representação
vetorial corresponde a linhas, pontos, e polígonos que definem as
formas de representação dos objetos espaciais, enquanto a
representação de varredura corresponde a uma matriz de pontos
com valores em cada célula. Os tipos de dados tratados no SPRING
são:
- Mapas temáticos: cada informação
representa um tema ou classe de informação. Por exemplo as
classes de uso do solo de uma região.
- Mapas cadastrais ou mapa de objetos:
ao contrário de um mapa temático, cada elemento é
um objeto geográfico, que possui atributos e que pode estar associado
a várias representações gráficas. Por exemplo,
os lotes de uma cidade são elementos do espaço geográfico
que possuem atributos (dono, localização, valor venal, IPTU
devido, etc.) e que podem ter representações gráficas
diferentes (poligonais, lineares, ou pontuais) em mapas de escalas distintas.
- Mapas de redes: correspondem a mapas
cadastrais, com a diferença de que geralmente os objetos são
representados por elementos lineares ou pontuais. As representações
pontuais devem estar localizadas em pontos de intersecção
de linhas na rede.
- Modelo numérico de terreno: denota
a representação de uma grandeza que varia continuamente no
espaço. Comumente associados à altimetria, podem ser utilizados
para modelar outros fenômenos de variação contínua
(como variáveis geofísicas, geoquímicas e batimetria).
- Imagens: representam dados de sensoriamento
remoto ou fotografias aéreas.
O algorítmo para localização das medianas
pode ser aplicado no SPRING em dados dos modelos temático, cadastral
e de redes, da forma descrita a seguir:
- Para uso em um dado temático é
necessário que a representação vetorial contenha pontos.
As localizações espaciais dos pontos e a distância
linear entre os mesmos são utilizados no processo de localização
das medianas.
- Para o dado cadastral o procedimento
de localização das medianas atua sobre uma determinada categoria
de objetos selecionada. Todos os objetos desta categoria que estejam associados
a uma representação pontual são utilizados na análise
de localização, que usa a distância linear entre os
pontos.
- Para o modelo de redes o modo de utilização
é similar ao do modelo cadastral, com a diferença de que
a distância entre os pontos pode ser escolhida entre linear, ou ser
computada a partir da própria rede.
A Figura 1 mostra a interface para execução
da função de localização de medianas no SPRING.
O cálculo das medianas usa a área da informação
que está visível no monitor. A partir de um plano de informação
ativo, o usuário define o número de medianas a serem calculadas.
Se o plano ativo corresponder a um dado temático esta é a
única informação necessária a ser fornecida,
sendo considerada a distância linear entre os pontos. Para o caso
de dados cadastrais ou de redes, a lista de categorias de objeto fica ativa
para que seja selecionado um tipo de objeto. A princípio apenas
objetos do mesmo tipo entram na análise de localização,
podendo esta restrição não existir em versões
futuras. O cálculo da distância entre os pontos corresponde
à distância linear para os modelos temático e cadastral,
enquanto que para o modelo de redes também está disponível
selecionar que a distância seja calculada baseada na própria
rede. Nesta primeira versão, esta interface também apresenta
a opção de se associar algum valor de demanda ou peso para
os pontos em análise, embora ainda esteja inibida. Este valor poderá
ser obtido a partir de um atributo no banco de dados.
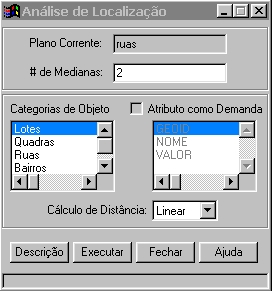
Fig. 1: Interface de diálogo para localização
de medianas no SPRING.
As Figuras 2 e 3 mostram os resultados da análise
de localização em uma pequena região da cidade de
São José dos Campos. Alguns objetos localizados em nós
da rede correspondem à possíveis localizações
para instalação de algum tipo de atividade. Dado o número
de medianas a se encontrar, o programa gera como resultado na tela, os
pontos correspondentes às medianas (representados por círculos)
e associa os outros pontos à mediana mais próxima. Pode-se
observar que os resultados considerando as distâncias linear e da
rede não necessáriamente são iguais.
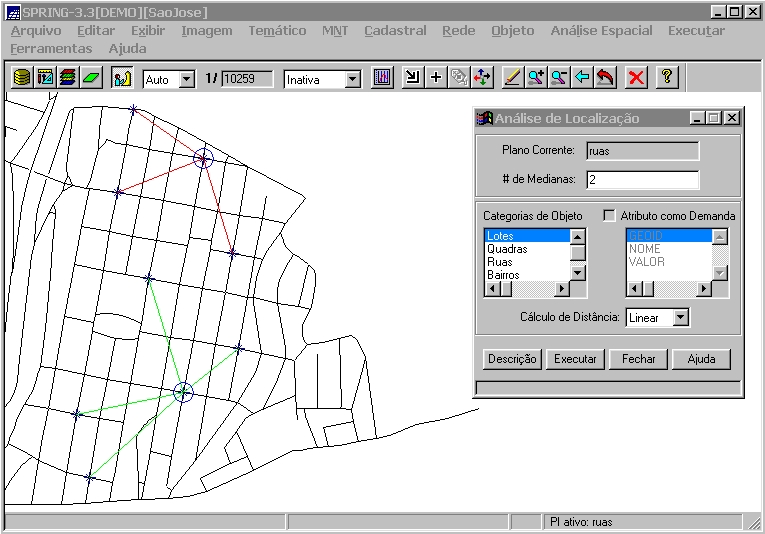
Fig. 2: Cálculo de medianas no SPRING usando distância
linear.
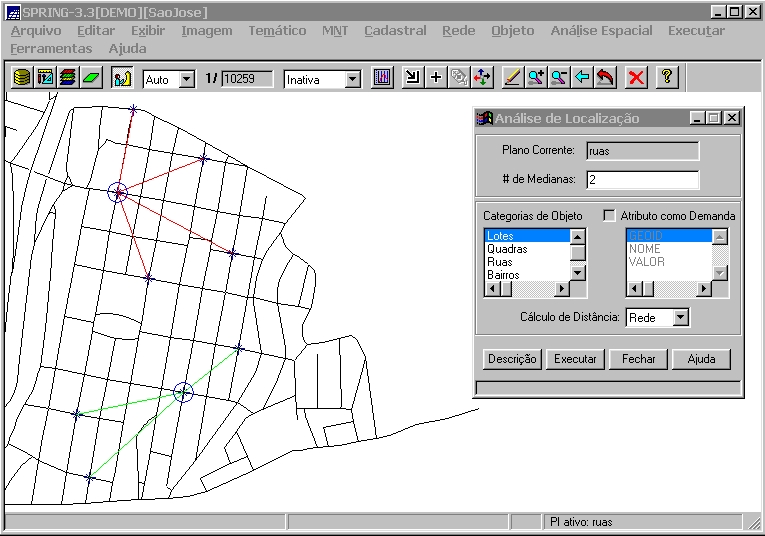
Fig. 3: Cálculo de medianas no SPRING usando distâncias
da própria rede.
Referências Bibliográficas
1. Câmara, G. Modelos, Linguagens e Arquiteturas
para Bancos de Dados Geográficos. Tese de Doutorado, INPE -
São José dos Campos, SP, 1995.
2. SPRING - Sistema de Processamento de Informações
Georeferenciadas, INPE, São José dos Campos, SP, http://www.dpi.inpe.br/spring,
1998.